More math with working graphs:
http://phdfootball.blogspot.com/2014/03/first-down-probability.html
First Down Probability
Abstract
In this post I compute the First Down Probability metric, which predicts how likely a drive will produce at least one more first down for a given down and distance. I find similar overall first down conversion rates to prior studies in the literature, including that third down rushing plays are significantly underutilized. Unlike previous studies, however, I break down these rushing plays by the position of the ballcarrier, and find that a significant portion of this discrepancy comes from rushes by the quarterback, likely from scrambles on broken passing plays. More puzzling is the fact that QB runs on first and second downs don't show this trend, a result that is difficult to convincingly explain.
Introduction
During the course of a football game a fan gets a lot of statistical information. These numbers – QB rating, a running back's average yards per carry, time of possession, etc – generally lack any kind of contextual information about how the game is actually going. At best these statistics are incomplete (showing a WR's average yards per catch after a 99-yard completion, for instance); at worst, they're downright misleading (That QB just had 5 completions in a row...but they were all screens for minimal yardage).
A better statistic is one that takes the game situation into account. For instance, a 5-yard completion should count for more on third and 4 than on third and 16. There are several such statistics already in existence, such as
Football Outsider's DVOA metric or
Expected Points. These sorts of metrics generally depend on using historical play-by-play data to compute average outcomes for plays at any given down and distance. This approach is (unsurprisingly) more computationally complex, and often can appear opaque to the casual fan. Some of these stats, such as the DVOA, are intricate enough that their creators have decided to keep the full details of their computation private.
A direct and (relatively) simple context-sensitive statistic is Brian Burke's
First Down Probability, which I will abbreviate as FDP. That link has more details, but the core insight of this metric is that the average odds of converting the next first down in a series can be estimated for any given down and distance. With this information in hand, it's possible to evaluate the result of a play based on whether it improves or harms the offense's chance of eventually getting a first down.
In this post I'm going to compute the FDP for the plays in the
Armchair Analysis database. One may ask why I would recompute this quantity when Burke has already done quite a good job of it. One reason is to ensure the reproducibility of results – while I trust Burke's analysis, everyone makes mistakes. A more basic reason is that while Burke produces a nice visualization of his computed FDP he doesn't provide his data in a tabular form, which makes using his FDP values difficult (at best). I can also extend the FDP calculation to all four downs (Burke only considers second and third downs in his post). Finally, I can (spoiler alert) start using FDP to generate new insights about how teams approach different down-and-distance situations.
Data
As I mentioned before, I'm using the Armchair Analysis database, which covers the 2000-2011 NFL seasons. I grabbed the play-by-play data for all regular season and playoff games, then filtered out plays for several reasons. Plays inside the two minute warnings were discarded because teams play differently in those situations; I removed plays when the game wasn't close (defined as one team being up by more than 16 points) for the same reason. I cut out all punts and field goals as well as penalties (although I keep the results of the penalties in the data: if a team runs for -5 yards on second down but then is the beneficiary of a 15-yard roughing the passer call on third down, the second down play would be considered as ultimately resulting in a first down for the purposes of this analysis). Finally, to avoid biasing the data based on field position I only include plays between the offense's own 10-yard line and the redzone.
Ultimately this results in a dataset of 262,601 plays, split 56%-44% in favor of passes over runs. I bin these plays as a function of current down and yards to go, eliminating bins with fewer than 200 plays in my dataset. This cut ensures that there are no bins with conversion rates dominated by
sampling error. The Python script I used to do this data querying and processing (as well as produce the plots in later sections) can be found
here.
Results
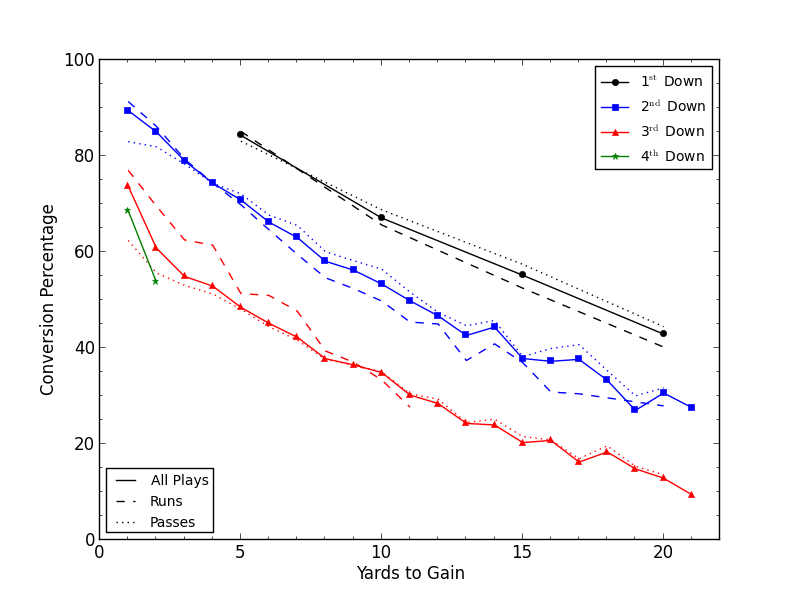
Figure 1: FDP as a function of down and distance. The colors denote different downs, while the line styles break down success if the next play in the drive is a run or a pass. In some cases the data for the individual types of plays does not cover the same range of yards to gain. This is due to the minimum play cutoff detailed in the Data section.
Figure 1 shows the raw results, split by down and distance. For the benefit of anyone looking to check my results or to build on them I have also tabulated these results in text files, which can be obtained
from my GitHub repository. Feel free to use them as long as you explain where you got them from (and a link back here would be nice as well!).
Anyway, the first thing to do is to check my results with what Burke
obtained. It's a bit difficult to compare directly since I can only eyeball our plots, but in general my results seem to be fairly copacetic with his. The data between downs look fairly similar, with a ~15% shift each down as you go from first and N to second and N, increasing to ~20% from second to third down. There's not much data on fourth down, but I see no reason why it wouldn't resemble the other downs for conversion attempts beyond 2 yards.
More interesting is what happens when you break the conversion percentages down by type of play. Note that when comparing the FDP of runs versus passes at a given down and distance, a higher conversion rate for e.g. a pass doesn't necessarily mean you should always throw the ball in that situation; rather, it implies that currently NFL teams are not playing at the
Nash equilibrium. This means that NFL teams should call
more passing plays in that situation than they currently do; as defenses adjust to this new reality, there should be more opportunities for successful rushing plays, and eventually the FDP of both types of plays will equalize. Burke has some more detailed discussion of this in his
breakdown of first down probability for runs and passes (although he restricts his analysis to third downs).
So again we are treading on old ground, and again it makes sense to compare results. Here we find a bit of a discrepancy, with Burke's rushing FDP on third and short ~5% lower than mine. It's not clear why this would be, although it might be due to the fact that Burke's data only goes through the 2007 season or how he considers sacks (the Armchair Analysis database considers sacks to just be really crappy passes). Regardless, things appear similar enough to proceed.
It's clear that teams aren't passing enough on first and second downs with more than 5 yards to go. Considering teams are already passing a lot in those situations, especially in second and 10+, this would imply that even the occasional rush in such circumstances is too much.
In short yardage, however, things are reversed. On second and 3 or less teams are running
less often than they 'should', although the difference is only at about 7% or so. Third down is even more striking: whenever there are fewer than 9 yards to go the data indicate that teams should be running more. This is an even larger discrepancy than Burke finds, and is downright shocking given how unusual 7+ yard runs are under normal circumstances.
But there are two kinds of runs – designed runs and aborted passing plays. Burke considers the latter category to be rare enough to be inconsequential, but I wasn't so certain. So I modified my program to separate out rushes by the position of the ballcarrier – it can't tell if a QB rush was designed that way or if it was improvised, but it's better than nothing.
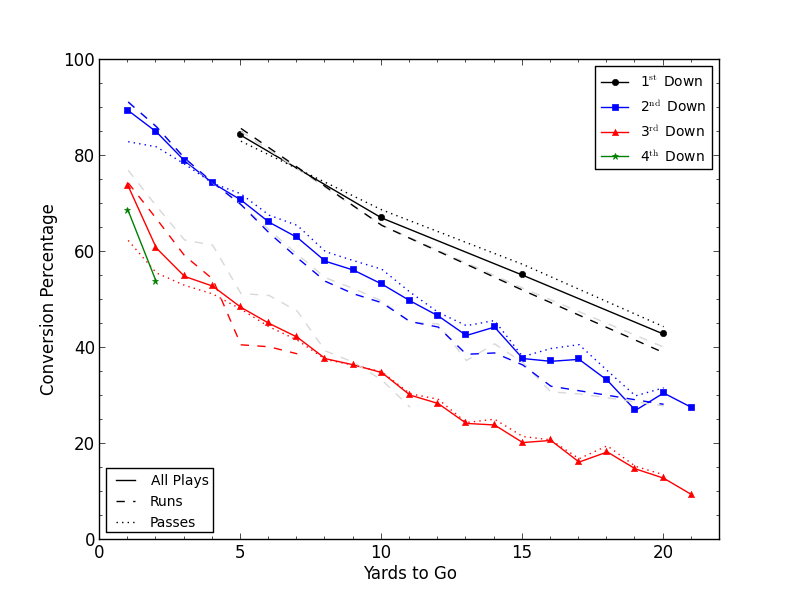
Figure 2: FDP, corrected for the influence of QB runs (the uncorrected rushing percentages are shown in gray to facilitate direct comparison).
Figure 2 shows the result, and it turns out that without the QB involved a third down rush becomes a much worse proposition. Indeed, now teams should only be running more on third and 3 or less, consistent with what the data show for second down.
While teams are generally doing better at finding the equilibrium between passes and rushes with RBs, these results indicate that teams are letting their signal-callers run the ball far too infrequently. If you look at the conversion rates just for QB scrambles it's generally 10% or more higher than a rush from a running back in the same situation! Even more interesting is that this offset
only applies on third down. On first and second down a QB scramble appears to have similar conversion rates as a regular rush.
Discussion and Conclusions
First of all, the fact that QB rushes are so underused compared to other types of plays is quite interesting. Given the fact that teams generally do not want their prize passers taking hits down the field, most of these successful conversions are likely due to scrambles on passing attempts. But given how high the conversion rate is perhaps coaches should consider running a few more QB draw plays, especially with all the mobile passers entering the league.
But what's really weird is that QB's rushes aren't more successful than the regular variety on earlier downs. A possible explanation is that defenses are more keyed toward stopping shorter-yardage plays on second down, whereas on third down they sit back and follow the WRs down the field. But in that case you would expect third down rushes to be equally successful, regardless of the runner. I think it's more likely that on second down a QB under pressure isn't concerned with making the sticks, but rather simply looks to get out of trouble. On third down, however, the consequences of playing it safe are much more clear, which encourages passers to scramble for every last yard.
Of course, I'll be the first to admit that this is just speculation. A definitive analysis of this phenomenon would probably require deep analysis of individual quarterback scrambles, which is way beyond the scope of this work. But it is a cool result from a (relatively) simple metric, and illustrates how deep insights can be gleaned from just a little bit of intelligent digging.
I actually periodically read this stuff.
I have no life.
For every series beginning with a 1st down and 10 in the NFL, an offense achieves another 1st down (including scoring a TD) 66% of the time. So if an offense is to be graded on a 1st down play, it should at least gain enough yards so that they have at least the same probability of sustaining the drive or scoring. In this article, I’ll begin a discussion of utility in football by examining the break even point in a series of downs. In other words, what would you rather have, a 1st and 10 or 2nd and 7? What about 2nd and 6? 5?
